变换和矩阵

3D网格是通过它们顶点的位置确定的。如果每次你想移到当前网格的另一个视角的时候都需要修改其顶点的位置将会是一件非常痛苦的事情，尤其是当这个网格不停运动的时候。也正因如此，大多数的3D系统都支持变换，通过变换，不需要遍历所有的顶点并修改其位置，仅需要修改几个相对顶点，即可移动一个网格。通过变换，我们无需修改网格顶点的任何值，即可以缩放，旋转，偏移这个网格。

图表1-5通过实际操作来展示3D变换。在这个示例中，我们看到三个立方体。这三个立方体的顶点值其实是一样的。我们仅仅通过变换在不修改顶点的前提下，就旋转，缩放，偏移了这些网格。左侧的红色立方体在x轴方向上向左移了4个单位，并在x轴和y轴上分别作了旋转。(旋转值我们使用弧度作单位，在第四章中将详细介绍。)右侧的蓝色立方体，往右移动了4个单位，并在三维空间内放大到了1.5倍。中间的绿色立方体没有做任何变换。

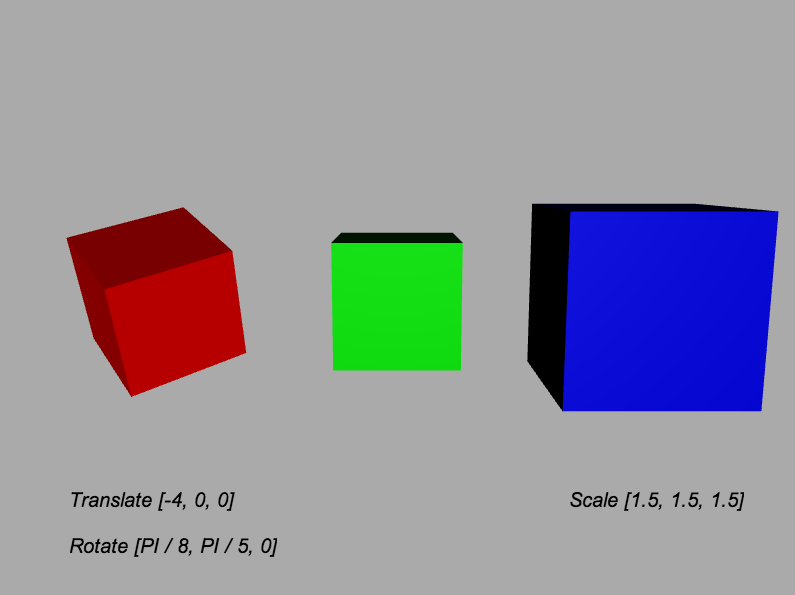
图表1-5. 3D变换：移位，旋转和缩放

一个3D变换可以被经典表示成一个变换矩阵，变换矩阵是一个包含一串用于计算变换顶点位置的值的数学体。大多数WebGL变换使用一个44的矩阵，一个4行4列包含16个值的数组。图表1-6展示了一个44矩阵的布局。存储在元素m12,m13,和m14上的值，分别对应x，y，z轴的移位值。x，y，和z的缩放值存储在矩阵对角线上m0，m5和m10元素上。x轴的旋转值存储在m1和m2上，y轴的旋转值存储在m4和m6上，z轴的旋转值存储在m8和m9上。用这个矩阵去乘以一个3D的矢量值最终将得到变换值。

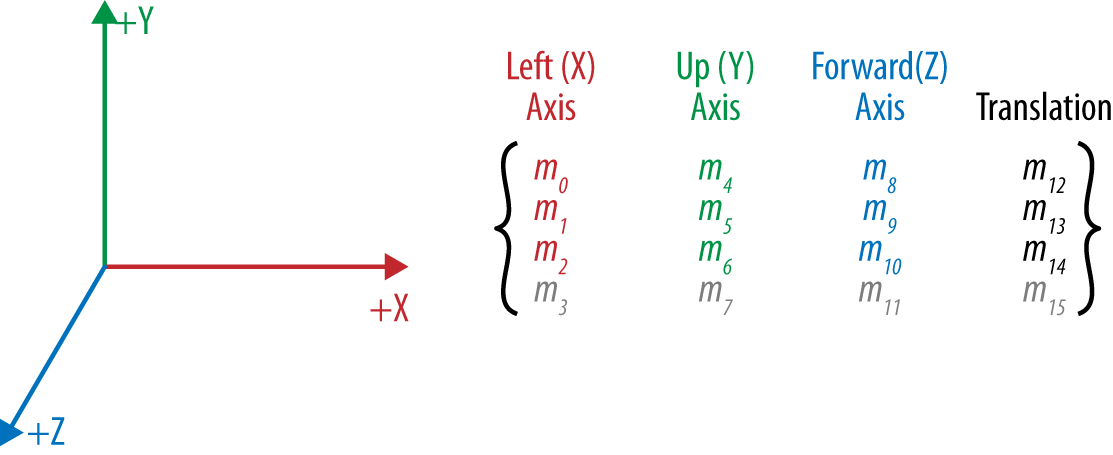图表1-6. 一个4*4的变换矩阵；被授权使用

如果你是一个如我一般对线性代数痴迷的人，理解上边的矩阵必然不会有问题。如果你不是，也无需灰心丧气。开发本书中示例程序的工具允许你把矩阵作为黑盒子来对待：我们只需要输入位移，旋转或者缩放，它会帮我处理余下的事情。